Answer:
Area of the gray region = 64 square units
Explanation:
Area of the white square = 64 square units
Length of a side of the given square =
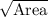
=
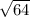
= 8 units
By Pythagoras theorem,
Length of diagonal DB =
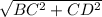
DB =
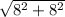
=
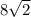
AD = DB =
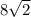 [Given]
[Given]
OD = OC =
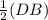
= 4√2
Therefore, AO = AD + OD = 8√2 + 4√2
= 12√2
Area of ΔACD = Area of ΔAOC - Area of ΔCOD
=

=
![(1)/(2)[(12√(2)* 4√(2))-(4√(2))^2]](https://img.qammunity.org/2022/formulas/mathematics/college/2xnep5dzkqf97tfrs3qv7af3ivpkblbaui.png)
=
![(1)/(2)[96-32]](https://img.qammunity.org/2022/formulas/mathematics/college/lhdkq3qmviuqnypr28r497eos39oj2qn65.png)
= 32
Therefore, area of gray part = Area of ΔACD + Area of ΔAED
= 32 + 32
= 64 square units