Question

It costs $1,400 to manufacture 100 designer shoes, and $4,100 to manufacture 400 designer shoes. If x represents the number of shoes, and y is the costs,

find the cost equation
What is the cost to manufacture 150 shoes
If the product sells for $19 per item; find the Revenue Function
Determine the number of items needed to break even.

Answer 1

To find the cost equation, we can use the two data points given:

(100, 1400) and (400, 4100)

We can use the point-slope form of a linear equation, where the slope is the change in cost over the change in quantity:

slope = (4100 - 1400) / (400 - 100) = 2700 / 300 = 9

Using the point-slope form with the first data point:

y - 1400 = 9(x - 100)

y - 1400 = 9x - 900

y = 9x + 500

So the cost equation is y = 9x + 500.

To find the cost to manufacture 150 shoes, we can plug in x = 150 into the cost equation:

y = 9(150) + 500 = 1850

So the cost to manufacture 150 shoes is $1850.

To find the revenue function, we multiply the number of shoes sold by the price per shoe:

Revenue = price x quantity = 19x

To determine the number of items needed to break even, we need to find the quantity where revenue equals cost. Let C(x) be the cost function and R(x) be the revenue function. The break-even point occurs when:

C(x) = R(x)

9x + 500 = 19x

500 = 10x

x = 50

So the company needs to sell 50 designer shoes to break even.

Explanation:

Answer 2

Cost equation: y = 9x + 500

It costs $1,850 to manufacture 150 shoes.

Revenue function: R(x) = 19x

The number of items that need to be sold to break even is 50.

Explanation:

Definition of variables

• x is the number of designer shoes manufactured.
• y is the cost (in dollars) to manufacture the designer shoes.

If it costs $1,400 to manufacture 100 designer shoes:

• x = 100 when y = 1400.

If it costs $4,100 to manufacture 400 designer shoes:

• x = 400 when y = 4100.

Assuming the relationship between the number of shoes and the cost to manufacture them is linear, the slope of the equation of the line the models the relationship can be found by dividing the change in y-values by the change in x-values of the two data points:

`\implies \sf Slope\;(m)=(y_2-y_1)/(x_2-x_1)=(4100-1400)/(400-100)=9`

Substitute the found slope and one of the points into the point-slope form of a linear equation to create an equation that gives the total cost to manufacture the shoes in terms of the number of shoes (x):

`\implies \sf y-y_1=m(x-x_1)`

`\implies \sf y-1400=9(x-100)`

`\implies \sf y-1400=9x-900`

`\implies \sf y=9x+500`

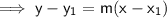
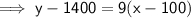
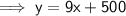
Therefore, the cost equation is y = 9x + 500.

To calculate the cost to manufacture 150 shoes, substitute x = 150 into the cost equation:

`\begin{aligned}\implies \sf y&=\sf 9(150)+500\\&= \sf 1350+500\\&= \sf 1850\end{aligned}`

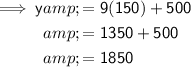
Therefore, it costs $1,850 to manufacture 150 shoes.

The revenue is the income a company generates before any expenses are subtracted. Therefore, the revenue function is simply the selling price of the item multiplied by the number of items sold.

Given the product sells for $19 per item, the revenue function is:

`\implies \sf R(x)=19x`

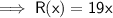
The break even point is the point at which the total revenue equals the total cost, so there is neither profit nor loss.

To determine the number of items that should be sold to break even, equate the cost equation and the revenue function and solve for x.

`\begin{aligned}\sf R(x)&=\sf y\\\implies \sf19x&=\sf 9x+500\\\sf 10x&=500\\\sf x&=50\end{aligned}`

Therefore, the number of items that need to be sold to break even is 50.