Question

Find all critical points for the function

4x + 6
x² + x + 1
on (-∞, ∞) and then list them (separated by commas) in the box below.
List of critical points:
f(x) =

Answer 1

Answer:
`(-3+√(7))/(2), \ (-3-√(7))/(2)`

========================================================

Step-by-step explanation:

Let

• g(x) = 4x+6
• h(x) = x^2+x+1

Each derivative is,

• g ' (x) = 4
• h ' (x) = 2x+1

which will be useful in the next section.

--------------

`f(\text{x}) = \frac{4\text{x}+6}{\text{x}^2+\text{x}+1} = \frac{g(\text{x})}{h(\text{x})}\\\\f(\text{x}) = \frac{g(\text{x})}{h(\text{x})}\\\\`

Apply the derivative with respect to x. We'll use the quotient rule.

`f(\text{x}) = \frac{g(\text{x})}{h(\text{x})}\\\\\\f'(\text{x}) = \frac{g'(\text{x})h(\text{x})-g(\text{x})h'(\text{x})}{\big[h(\text{x})\big]^2}\\\\\\f'(\text{x}) = \frac{4(\text{x}^2+\text{x}+1)-(4\text{x}+6)(2\text{x}+1)}{(\text{x}^2+\text{x}+1)^2}\\\\`

The critical value(s) occur when either...

• f ' (x) = 0
• f ' (x) doesn't exist, when x is in the domain of f(x)

The first criteria will be handled in the next section.

The second criteria is handled in the section after that.

-------------------------

f ' (x) is in the format A/B. It means f ' (x) = 0 leads to A/B = 0 and A = 0.

We set the numerator equal to zero and solve for x.

`4(\text{x}^2+\text{x}+1)-(4\text{x}+6)(2\text{x}+1) = 0\\\\4(\text{x}^2+\text{x}+1)-(8\text{x}^2+16\text{x}+6) = 0\\\\4\text{x}^2+4\text{x}+4-8\text{x}^2-16\text{x}-6 = 0\\\\-4\text{x}^2-12\text{x}-2 = 0\\\\-2(2\text{x}^2+6\text{x}+1) = 0\\\\2\text{x}^2+6\text{x}+1 = 0\\\\`

From here we use the quadratic formula.

Plug in a = 2, b = 6, c = 1.

`\text{x} = (-b\pm√(b^2-4ac))/(2a)\\\\\text{x} = (-6\pm√((6)^2-4(2)(1)))/(2(2))\\\\\text{x} = (-6\pm√(28))/(4)\\\\\text{x} = (-6\pm2√(7))/(4)\\\\\text{x} = (2(-3\pm√(7)))/(4)\\\\\text{x} = (-3\pm√(7))/(2)\\\\\text{x} = (-3+√(7))/(2) \text{ or } \text{x} = (-3-√(7))/(2)\\\\`

If x is equal to either of those values, then f ' (x) = 0 would be the case. Therefore, these are the critical points of f(x).

There may be other critical values. We'll still need to check the second criteria.

-------------------------

f ' (x) doesn't exist when we divide by zero.

Set the denominator equal to 0 and solve for x.

`(\text{x}^2+\text{x}+1)^2 = 0\\\\\text{x}^2+\text{x}+1 = 0\\\\`

Plug a = 1, b = 1, c = 1 into the quadratic formula.

`x = (-b\pm√(b^2-4ac))/(2a)\\\\x = (-1\pm√((1)^2-4(1)(1)))/(2(1))\\\\x = (-1\pm√(-3))/(2)\\\\`

We have a negative number as the discriminant, which leads to complex number solutions in the form a+bi where
`i = √(-1)`

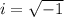
Therefore, there aren't any real number values for x that lead
`(\text{x}^2+\text{x}+1)^2` to be zero.

No matter what we pick for x, the expression
`(\text{x}^2+\text{x}+1)^2` will never be zero.

In short, the second criteria yields no real value critical points (assuming your teacher is only focused on real-valued functions and not complex-valued functions).

-------------------------

Summary:

• The first criteria f ' (x) = 0 led to
  `\text{x} = (-3+√(7))/(2) \text{ or } \text{x} = (-3-√(7))/(2)` as the critical values
• The second criteria, f ' (x) doesn't exist where x is in the domain of f(x), leads to no critical values (assuming your teacher is not focusing on complex-valued functions).

Therefore, the only critical values are
`\text{x} = (-3+√(7))/(2) \text{ or } \text{x} = (-3-√(7))/(2)`

-------------------------

Extra info:

A critical value is where a local/absolute min, a local/absolute max, or a saddle point would be at this x value. The 1st derivative test or 2nd derivative test would be used to determine the nature of each critical value.

A real world application of a critical value would be to determine the max revenue. Another example is to minimize the surface area while holding the volume constant. Linear regression relies on a similar concept.

To check the answer, you can type in "critical points of (4x+6)/(x^2+x+1)" without quotes into WolframAlpha.