Question

Can you please answer the questions and explain how you got it?

Answer 1

Given data:

The mass of the block on table is M=500 g.

The hanging mass is m=300 g.

The kinetic friction is μ=0.25.

Part (a)

The free body diagram of the block on table is shown below,

The free body diagram of hanging mass is shown below,

Part (b)

The equation according Newton's second law for 500 g mass will be,

`\begin{gathered} F_(net)=Ma \\ T-f=Ma \\ T-\mu N=Ma \\ T-\mu Mg=Ma \\ T=M(a+\mu g)\ldots\ldots(1) \end{gathered}`

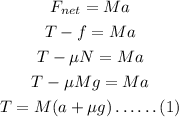
Here, f is the friction force, N is the normal force, and T is the tension in the string.

Part (c)

The equation according Newton's second law for 300 g mass will be,

`\begin{gathered} F_(net)=ma \\ mg-T=ma \\ T=mg-ma \\ T=m(g-a)\ldots\ldots(2) \end{gathered}`

Part (d)

Equating equation (1) and (2) to solve for acceleration,

`\begin{gathered} M(a+\mu g)=m(g-a) \\ 500(a+0.25(9.81))=300(9.81-a) \\ a+2.45=0.6(9.81-a) \\ a+2.45=5.886-0.6a \\ a+0.6a=5.886-2.45 \\ 1.6a=3.436 \\ a=2.14m/s^2 \end{gathered}`

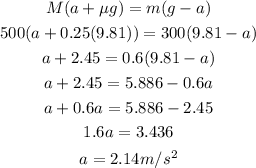
Thus, the acceleration of the blocks are 2.14 m/s².

Part (e)

Substitute the value of acceleration in equation (1) to calculate the tension,

`\begin{gathered} T=M(a+\mu g) \\ T=500(2.14+(0.25)(9.81)) \\ T=2296gm/s^2*\frac{1\text{ N}}{1000gm/s^2} \\ T=2.296\text{ N} \end{gathered}`

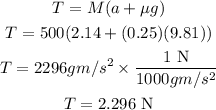
Thus, the tension in the sting is 2.296 N.