Question

NEED ASAP!!!!!!!!!!!!!!!!!1 Identify the formula used to find total surface area, then calculate total surface area. Select the appropriate choices.

Formula:


Total Surface Area:

Answer 1

The total surface area of the triangular prism is 556 square units.

Explanation:

The given 3D figure is a triangular prism.

The formula to find the total surface area of a triangular prism is:

`\boxed{\textsf{Total Surface Area}= \sf 2 A_B+(a+b+c)h}`

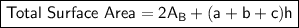
where:

• 
  `\sf A_B` is the area of one of the triangular bases.
• a, b and c are the side lengths of the triangular bases.
• h is the height of the prism.

Therefore, the surface area of a triangular prism is the sum of the area of two congruent triangular bases and three rectangles.

The area of a triangle can be calculated by halving the product of the length of its base and height.

The base of the triangles is 17 units and the height is 8 units.

Therefore, the area of each triangular base is:

`\begin{aligned}\implies \sf Area\;of\;triangular\;base\;(A_B)&=\sf(1)/(2) \cdot17 \cdot8\\&=\sf 68\;square\;units\end{aligned}`

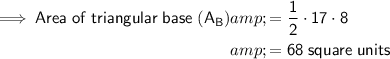
Therefore, the values to substitute into the total surface area formula are:

• a = 11
• b = 14
• c = 17
• h = 10
• 
  `\sf A_B = 68`

`\begin{aligned}\implies \textsf{Total Surface Area}&= \sf 2 A_B+(a+b+c)h\\&= \sf 2 (68)+(11+14+17)10\\&=\sf 2 \left(68\right)+(42)10\\&=\sf 136+420\\&=\sf 556 \; square\;units\end{aligned}`

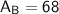
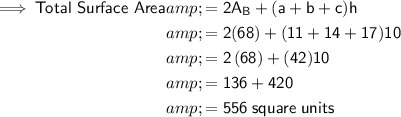
Therefore, the total surface area of the given triangular prism is 556 square units.