Question

The mean height of men is known to 5.9 ft with a standard deviation of 0.2 ft. The height of a man (in ft) corresponding to a z-score of 2 is:Group of answer choices6.16.36.25.9

Answer 1

The average height is μ= 5.9ft and has a standard deviation of σ=0.2ft.

You have to determine the height (X) for the Z-score z=2

To determine this value, you have to use the formula of the standard deviation:

`Z=(X-\mu)/(\sigma)`

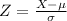
First, write the equation for X:

-Multiply both sides by sigma:

`\begin{gathered} Z\sigma=\sigma(X-\mu)/(\sigma) \\ \\ Z\sigma=X-\mu \end{gathered}`

-Add mu to both sides of it:

`\begin{gathered} (Z\sigma)+\mu=X-\mu+\mu \\ X=(Z\sigma)+\mu \end{gathered}`

Replace the expression obtained for X with the known values of z, sigma, and mu

`\begin{gathered} X=2\cdot0.2+5.9 \\ X=\text{0}.4+5.9 \\ X=6.3 \end{gathered}`

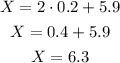
The height of a man that corresponds to z=2 is 6.3 ft