Question

Tom wishes to purchase a property that has been valued at $300,000. He has 25% of this amount available as a cash deposit, and will require a mortgage for the remaining amount. The bank offers him a 25-year mortgage at 2% interest. Calculate his monthly payments.

Round your answer to the nearest cent.
Do NOT round until you have calculated the final answer.

Answer 1

so hmmm 25% of that 300,000 is going as a downpayment, so he need the loan for the remaining 75% of that hmmm

`\begin{array}ll \cline{1-1} \textit{\textit{\LARGE a}\% of \textit{\LARGE b}}\\ \cline{1-1} \\ \left( \cfrac{\textit{\LARGE a}}{100} \right)\cdot \textit{\LARGE b} \\\\ \cline{1-1} \end{array}~\hspace{5em}\stackrel{\textit{75\% of 300000}}{\left( \cfrac{75}{100} \right)300000}\implies 225000`

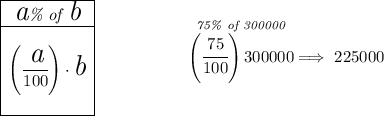
so for that much, so since he'll be making monthly payments, the compounding period will be monthly, now, we're assuming the payments are at the end of each month.

`~~~~~~~~~~~~\underset{\textit{payments at the end of the period}}{\textit{Payments of an ordinary annuity}} \\\\ pmt=A\left[ \cfrac{(r)/(n)}{\left( 1+(r)/(n) \right)^(nt)-1} \right]`

`\begin{cases} A=\textit{accumulated amount}\dotfill &225000\\ pmt=\textit{periodic payments}\\ r=rate\to 2\%\to (2)/(100)\dotfill &0.02\\ n= \begin{array}{llll} \textit{times it compounds per year}\\ \textit{monthly, thus twelve} \end{array}\dotfill &12\\ t=years\dotfill &25 \end{cases}`

`pmt=225000\left[ \cfrac{(0.02)/(12)}{\left( 1+(0.02)/(12) \right)^(12 \cdot 25)-1} \right] \\\\\\ pmt=225000\left[ \cfrac{(1)/(600)}{\left( (601)/(600) \right)^(300)-1} \right]\implies pmt\approx 578.67`

Answer 2

Total interest is $149,528.31
Explanation:
In the first place,Tom already has 25%*$300,000=$75,000
This implies that the mortgage amount=$300,000-$75,000=$225,000
In order to ascertain the total interest Tom would pay it would necessary to know the total amount Tom would have to pay back in respect of the mortgage since the total interest is the difference between total amount repayable less the present worth of the mortgage of $225,000
FV=PV*(1+r)^n
FV is the future worth of the mortgage i.e total amount repayable
PV is the present worth of $225,000
r is the rate of interest of 2% yearly,but 0.17% monthly(2%/12)
n is the number of month it would take Tom to repay the mortgage i.e 25 years multiplied by 12 300 months
FV=$225,000*(1+0.17%)^300=$ 374,528.31
Total interest=$ 374,528.31-$225,000=$149,528.31