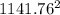Question

Help me! I need help with my homewor!

Answer 1

Area of shaded region= 1142.96mm²

Explanation:

•First calculate the Area covered by the interior circle.

•To calculate the Area of the exterior circle first add the two radii to get the radius from the centre of the interior circle to the circumference of the exterior circle.

•Use the calculated radius to calculate the Area covered from the centre to the circumference of the exterior circle.

•Now subtract the Area of the interior circle from the area covered by the bigger circle to get the Area of the shaded region.

Answer 2

1141.76

Explanation:

To solve for the area of the entire circle, we must first solve for the radius. Adding 6 and 14 will get us the total radius of the circle.

• 6 + 14 = 20

Therefore, the radius of the entire circle is 20.

The expression you can use to solve for the area of a circle is:

• Area = π × radius²

Inserting the radius into the expression:

• Area = π × 20²

Therefore, the area of the entire circle is 400π.

If there is a hole in the circle in the shape of a circle, we must subtract the area of that hole to find the area of the shaded region.

Inserting 6 into the expression to solve for area:

• Area = π × 6²

Therefore, the area of the hole is 36π.

Now, we need to subtract the area of the gap from the area of the entire circle.

• 400π - 36π = 364π

Because π is approximately equal to 3.14, we can calculate an approximate value for 364π by multiplying 364 by 3.14. This gives us:

• 364 × 3.14 = 1141.76.

Therefore, the area of the shaded region is
`1141.76^(2)`