Question

High order thinking and assessment practice

HELP PLS

Answer 1

10)

a) 5x + 5(11) = 120

b) x = 13

11) $392.50

12) Letter D

Explanation:

10:

5x + 5(11) = 120

5x + 55 = 120 Subtract 55 from both sides

5x + 55 - 55 = 120 - 55

5x = 65 Divide both sides by 5

`(5x)/(5)` =
`(65)/(5)`

x = 13

11:

Let j = Jason's earnings

Let k = Kevin's earnings

j = 212.50

k = 2j - 32.50

substitute 212.50 for j in the second equation and solve for k

k = 2(212.50)- 32.50

k = 425 - 32.50

k = 392.50

Kevin earned $392.50.

12:

18 =
`(1)/(2)` x + 6 Subtract 6 from both sides

18 - 6 =
`(1)/(2)` x + 6 - 6

12 =
`(1)/(2)` x Multiply both sides by 2

12(2) =
`(1)/(2)` x (
`(2)/(1)`) (
`(2)/(1)` is another name for 2)

24 = x

To solve we subtract 6 first and then multiply by 2. Letter D.

Helping in the name of Jesus.

Answer 2

High order thinking:

PART A:

If each friend buys 11 more action figures, then each will have x + 11 action figures. Since the total action figures is 120, we can write the equation:

`5(x+11)=120`

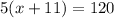
PART B:

Solve for x. Divide both sides by 5.

`x+11=24`

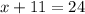
Substract 11 from both sides:

`x=13\\`

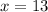
Each friend originally had 13 action figures each.

Assessment practice:

11: Let Kevin Earns X amount

So, Jason earns = 2x - 32.50

= 212.50

2x = 2120 x 50 +32.40 = 245.00/2

= 122.5

Answer: Kevin Earns $122.50

12: Subtract 6. Then multiply by 2.

`(1)/(2) x+6=18\\\\(1)/(2)x = 18-6\\(1)/(2)x=12\\(1)/(2)x*2=12*2\\x=24`

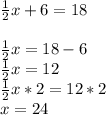
Thanks,
Eddie E.