Question

Determine the length of x in the triangle. Give your answer to two decimal places. Show the steps, please.

Answer 1

35.09 units

Explanation:

This is a right-angled triangle where:

Hypotenuse = x units

With respect to angle 20°:

Opposite = 12 units

Use trigonometric function sinФ to solve for x:

sinФ =
`(Opposite)/(Hypotenuse)`

∴sin20° =
`(12)/(x)`

Cross-multiplication is applied:

`(x)(sin20) = 12`

x has to be isolated and made the subject of the equation:

∴
`x = (12)/(sin20)`

x = 35.09 units (Rounded to 2 decimal places)

Answer 2

The length of x is 35.09 units to two decimal places.

Explanation:

In the given right triangle, we have been given the length of the side opposite the angle and need to find the length of the hypotenuse.

To find the value of x, use the sine trigonometric ratio.

`\boxed{\begin{minipage}{9 cm}\underline{Sine trigonometric ratio} \\\\$\sf \sin(\theta)=(O)/(H)$\\\\where:\\ \phantom{ww}$\bullet$ $\theta$ is the angle. \\ \phantom{ww}$\bullet$ $\sf O$ is the side opposite the angle. \\\phantom{ww}$\bullet$ $\sf H$ is the hypotenuse (the side opposite the right angle). \\\end{minipage}}`

Substitute θ = 20°, O = 12 and H = x into the ratio and solve for x:

`\implies \sin 20^(\circ)=(12)/(x)`

`\implies x=(12)/(\sin 20^(\circ))`

`\implies x=35.085652...`

`\implies x=35.09\; \sf (2\;d.p.)`

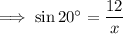
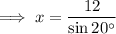
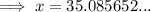
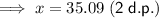
Therefore, the length of x is 35.09 units to two decimal places.