Question

Brookfield Street and Bloomington Avenue intersect. If Brookfield Street is 5 meters wide and Bloomington Avenue is 6 meters wide, what is the distance between two opposite corners of the intersection? If necessary, round to the nearest tenth.

Please respond
Thank you!

Answer 1

7.8m

Explanation:

To find:-

• The distance between opposite corners of intersection.

Answer:-

From the given data i made a figure to represent the given situation. To find the distance between the opposite corners we would have to use Pythagoras theorem, .

The distance between the corners represents the hypotenuse of the right angled triangle and another two sides are represented by 5m and 6m .

According to Pythagoras theorem,

`\rm\implies a^2+b^2 = h^2 \\`

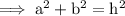
Here a is 5m and b is 6cm .

`\rm\implies (5m)^3+(6m)^2 = h^2 \\`

`\rm\implies 25m^2+36m^2=h^2\\`

`\rm\implies 61m^2=h^2\\`

`\rm\implies h =√(61m^2) \\`

`\rm\implies \red{ h = 7.8 \ m } \\`

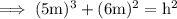
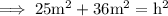
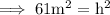
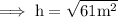
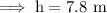
Hence the distance between the opposite corners is 7.8 m

Answer 2

Answer:7.8

Explanation:

`√(6^2+5^2)`

evaluate the equation / expression

7.81025

Round 7.81025 to the required place

7.8