Question

In Princeton, the library is due south of the courthouse and due west of the community swimming pool. If the distance between the library and the courthouse is 7 miles and the distance between the courthouse and the city pool is 8 miles, how far is the library from the community pool? If necessary, round to the nearest tenth.

Please respond.

Thank you!

Answer 1

3.9 miles

Explanation:

To find:-

• Distance between library and community pool .

Answer:-

The given situation is represented in the attachment.

We can see that there is a formation of right angled triangle , hence we can use Pythagoras theorem here , according to which,

`\rm\implies a^2+b^2=h^2 \\`

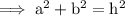
where h is the longest side (hypotenuse) of the triangle of the triangle . From the attached figure we can see that 8miles is hypotenuse and one of the other side is 7miles .

On substituting the respective values, we have;

`\rm\implies 7^2+b^2=8^2 \\`

`\rm\implies 49+b^2=64 \\`

`\rm\implies b^2 = 64-49\\`

`\rm\implies b =√(15)\\`

`\rm\implies \red{b = 3.9 } \\`

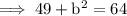
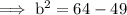
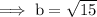
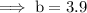
Hence the distance between the swimming pool and the Library is 3.9 miles .

Answer 2

We can see that the library, courthouse, and pool form a right-angled triangle. Using the Pythagorean theorem, we can find the distance between the library and the pool:

library-pool distance^2 = courthouse-library distance^2 + courthouse-pool distance^2

library-pool distance^2 = 7^2 + 8^2

library-pool distance^2 = 49 + 64

library-pool distance^2 = 113

library-pool distance = sqrt(113)

library-pool distance ≈ 10.6 miles

Therefore, the library is approximately 10.6 miles away from the community pool.