Question

7. The sides of a rectangle are in the ratio 5:2. If the perimeter of the rectangle is 42 cm, find the area of the rectangle.​

Answer 1

90 cm²

Explanation:

Let the greater side be the length L and the smaller side the width W

Given L : W = 5 : 2

we can rewrite this as a fraction

`(L)/(W) = (5)/(2)`

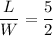
Cross-multiplying we get
2L = 5W

The perimeter of a rectangle
= 2(L + W)
= 2L + 2W
and we are told it is 42 cm

Therefore
2L + 2W = 42

Substitute 5W for 2L to get

5W + 2W = 42
7W = 42

or

W = 42/6 = 6

Given 2L + 2W = 42, substitute 6 for W to get

2L + 2(6) = 42

2L + 12 = 42

2L = 42 - 12= 30

L = 30/2 = 15

So length L = 15

Just to check
L/W = 15/6 = 5/2 by dividing both numerator and denominator by 3

Area of the rectangle
= L x W

= 15 x 6

= 90 cm²