Answer:
D) 8 + 4 + 2 + 1 + 1/2 + ...
Explanation:
The sum of an infinite geometric series can be found when the absolute value of the common ratio, r, is less than 1.

To determine which of the given infinite geometric series can be summed using the formula, calculate the value of r for each series. To do this, divide a term by the previous term.
Given infinite geometric series:
- -2 + 6 + (-18) + 54 + (-162) + ...

As r is not in the interval −1 < r < 1, the sum of the infinite series cannot be found using the formula.
Given infinite geometric series:
- 3 + 12 + 48 + 192 + 768 + ...
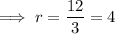
As r is not in the interval −1 < r < 1, the sum of the infinite series cannot be found using the formula.
Given infinite geometric series:
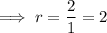
As r is not in the interval −1 < r < 1, the sum of the infinite series cannot be found using the formula.
Given infinite geometric series:
- 8 + 4 + 2 + 1 + 1/2 + ...
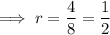
As |r| < 1 the sum of the infinite series can be found using the formula.
Therefore, the infinite series for which the sum can be found by using the formula is:
- D) 8 + 4 + 2 + 1 + 1/2 + ...