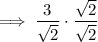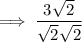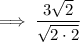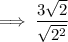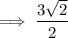Question

Simplify the given expression, and most importantly show the steps, please.

Answer 1

`(3√(2) )/(2)`

Explanation:

`(6)/(√(8) ) =(6)/(√(4*2) ) =(6)/(√(4)*√(2) )=(6)/(2*√(2) )= (3)/(√(2) )`

I simplified it leaving 3/sqrt(2).

We can not leave the denominator sqrt(2) for some reason due to a rule that i forgot.

`(3)/(√(2) )*(√(2) )/(√(2) ) =(3*√(2) )/(√(2)* √(2) ) =(3√(2) )/((√(2))^2 ) =(3√(2) )/(2)`

Answer 2

`(3√(2))/(2)`

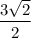
Explanation:

To simplify the given rational expression, first rewrite 8 as a product of prime numbers.

`\implies \sf 8 = 2 \cdot 2 \cdot 2`

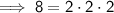
As we know that
`√(a^2)=a`, rewrite 8 as 2² · 2:

`\implies (6)/(√(2^2 \cdot 2))`

`\textsf{Apply radical the rule:} \quad √(ab)=√(a)√(b)`

`\implies (6)/(√(2^2) √(2))`

`\textsf{Apply radical the rule:} \quad √(a^2)=a, \quad a \geq 0`

`\implies (6)/(2√(2))`

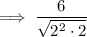
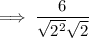
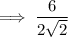
Rewrite 6 as a product of prime numbers:

`\implies (2 \cdot 3)/(2√(2))`

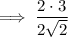
Cancel the common factor 2:

`\implies (\diagup\!\!\!\!2 \cdot 3)/(\diagup\!\!\!\!2√(2))=(3)/(√(2))`

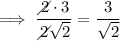
For a fraction to be in simplest form, the denominator should not be irrational.

To rationalize the denominator (get rid of the radical in the denominator), multiply the numerator and denominator by the radical of the denominator:

`\implies (3)/(√(2)) \cdot (√(2))/(√(2))`

`\implies (3√(2))/(√(2)√(2))`

`\textsf{Apply radical the rule:} \quad √(a)√(b)=√(ab)`

`\implies (3√(2))/(√(2 \cdot 2))`

`\implies (3√(2))/(√(2^2))`

`\textsf{Apply radical the rule:} \quad √(a^2)=a, \quad a \geq 0`

`\implies (3√(2))/(2)`