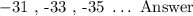Question

Find three consecutive odd integers that add to - 99

Answer 1

We will investigate how three consecutive odd numbers add up to a certain value.

We will assign a variable to the first odd number as follows:

`1st\text{ : x}`

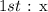
The next consecutive odd number will occur two integers ahead or two integers before the first odd number. We can choose either ( ahead or before ) and express second consecutive odd number in terms of first odd number as follows:

`2nd\colon\text{ ( x + 2 ) OR ( x - 2 )}`

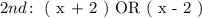
Similarly, the next consecutive odd number will occcur two integers ahead or two integer before the second odd number OR four integers ahead of for integers before the first odd number. We can choose either ( ahead or before ) and express the third consecutive odd number in terms of first or second odd number as follows:

`3rd\colon\text{ ( x + 4 ) OR ( x - 4 )}`

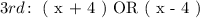
We will now sum up all three consecutive odd numbers and equate the result to ( -99 ) as follows:

`\begin{gathered} (\text{ x ) + ( x + 2 ) + ( x + 4 ) = -99} \\ OR \\ (\text{ x ) + ( x - 2 ) + ( x - 4 ) = -99} \end{gathered}`

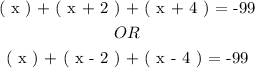
Then we will solve both possibilities step by step.

`\begin{gathered} 3x\text{ + 6 = -99} \\ OR \\ 3x\text{ - 6 = -99} \\ \end{gathered}`

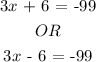
Then,

`\begin{gathered} 3x\text{ = -105} \\ OR \\ 3x\text{ = -93} \end{gathered}`

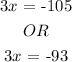
Next,

`\begin{gathered} x\text{ = }(-105)/(3)\text{ = -35} \\ \\ OR \\ \\ x\text{ = }(-93)/(3)\text{ = -31 } \end{gathered}`

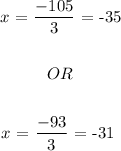
For each possibilitiy the three consecutive odd numbers would be:

`\begin{gathered} x\text{ = -35 , x + 2 = -33 , x + 4 = -31} \\ OR \\ x\text{ = -31 , x - 2 = -33 , x - 4 = -35} \end{gathered}`

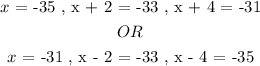
We see that both possibilities result in identical three consecutive odd numbers that would add up to a total of ( -99 ). Therefore, the three consecutive odd numbers are:

`-31\text{ , -33 , -35 }\ldots\text{ Answer}`