Answer:
Volume occupied by oxygen gas at 15 degree centigrade is equal to
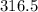 centimeter cube
centimeter cube
Step-by-step explanation:
Assuming Pressure is constant.
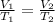
where T1 and T2 are temperature in Kelvin
Substituting the give values we get-
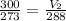
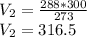
Volume occupied by oxygen gas at 15 degree centigrade is equal to
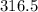 centimeter cube
centimeter cube