Question

Sara borrowed $5,500 at the beginning of her freshman year and another $4,500 at the beginning of her junior year. The interest rate (APR) is 6% per year, compounded monthly; Sara's interest accumulates at 0.5% per month. Sara will repay what she owes as an ordinary annuity over 60 months, starting one month after she graduates in the summer term of her fourth full year of college. Click the icon to view the interest and annuity table for discrete compounding when i = 0.5% per month. a. How much money does Sara owe upon graduation if she pays off monthly interest during school? Sara owes $ . (Round to the nearest dollar.) b. How much money does Sara owe if she pays no interest at all during her school years? Sara owes $ (Round to the nearest dollar.)

c. After graduation, what is the amount of the monthly loan repayment in Parts (a) and (b)? Monthly payment with interest repaid each month is $(Round to the nearest cent.) Monthly payment with no interest repaid is $(Round to the nearest cent.) d. How much interest does Sara repay without interest payments during school and with interest payments while in college? The total interest with interest paid while in school is $ (Round to the nearest dollar.) The total interest with no interest paid while in school is $ (Round to the nearest dollar.)

Answer 1

Sara owes $12100 upon graduation with monthly interest payments, $10000 without, pays $263.61/month with interest, $225.46/month without, and pays $3717/$3528 interest respectively.

How is that so?

Part a: Amount owed with monthly interest payments

Calculate the total loan amount: $5500 + $4500 = $10000

Calculate the monthly interest rate: 6% / 12 = 0.5%

Calculate the number of interest periods before graduation: 4 years * 12 months/year - 6 months (summer term) = 42 months

Calculate the interest accrued during school: $10000 * 0.005 * 42 = $2100

Add the accrued interest to the loan amount: $10000 + $2100 = $12100

Sara owes $12100 upon graduation if she pays off monthly interest during school.

Part b: Amount owed with no interest payments

Simply add the loan amounts: $5500 + $4500 = $10000

Sara owes $10000 if she pays no interest at all during her school years.

Part c: Monthly loan repayment

Use the loan repayment formula: Monthly Payment =
`P * (r * (1 + r)^n) / ((1 + r)^n - 1)`

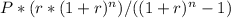
• P is the loan amount ($12100 for part a and $10000 for part b)
• r is the monthly interest rate (0.005)
• n is the total number of payments (60 months)

Calculate the monthly payment with interest:
`$12100 * (0.005 * (1 + 0.005)^60) / ((1 + 0.005)^60 - 1) = $263.61`

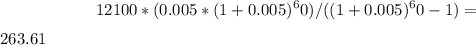
Calculate the monthly payment with no interest:
`$10000 * (0.005 * (1 + 0.005)^60) / ((1 + 0.005)^60 - 1) = $225.46`

Monthly payment with interest repaid each month is $263.61.

Monthly payment with no interest repaid is $225.46.

Part d: Total interest repaid with different scenarios

Interest with payments during school:

Calculate the total loan payment: $263.61 * 60 months = $15816.60

Calculate the total interest paid: $15816.60 - $12100 = $3716.60 (round to nearest dollar)

Interest with no payments during school:

Calculate the total loan payment: $225.46 * 60 months = $13527.60

Calculate the total interest paid: $13527.60 - $10000 = $3527.60 (round to nearest dollar)

The total interest with interest paid while in school is $3717.

The total interest with no interest paid while in school is $3528.