Question

A cannon ball is fired horizontally with a velocity of 50m/s from the top of a cliff 90m high.

a. After how many seconds will it strike the plain at the foot of the cliff?
b. At what distance from the foot of the cliff will it strike?
c. With what velocity will it strike the ground?

Answer 1

a. time of flight = 4.285 s

b. horizontal distance reached = 214.25m

c. final velocity = 65.3m/s, at 40° downwards

Step-by-step explanation:

This is a projectile motion question.

Things to note, in all projectile motion questions:

• in the horizontal component, velocity is always constant. There is no horizontal acceleration.
• at maximum height reached by the object, vertical velocity = zero
• the only vertical acceleration, is acceleration due to gravity = 9.8 m/s²
• vertical displacement, is initial height minus final height. ΔS

In projectile motion questions, we will use the three equations of motion:

`v=u+at\\v^2=u^2+2as\\s=ut+(1)/(2)at^2`

Thus we can adjust our equations for the x - component:

`v=u\\s=ut`, since acceleration = 0

For the y - component:

`v=u-gt\\v^2=u^2-2gs\\s=ut-(1)/(2)gt^2`, since acceleration = gravity (9.8 m/s²), downwards.

Now, with our question, we can note: u(x) = 50m/s, and u(y) = 0, since, initially, only horizontal motion. Also, s(y) = - 90m.

(a) After how many seconds will it strike the plain at the foot of the cliff?

In this question, we are asked to find time of flight, 't'. As we have s(y), u(y), and g, we can use the third equation,
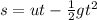`s=ut-(1)/(2)gt^2` to find t.

Since u=0, thus, - 90 = -1/2×9.8×t². solving this algebraically, therefore, time of flight = 4.285 s.

(b) At what distance from the foot of the cliff will it strike?

Now, we need to find the horizontal distance or range. All we can use to do this is s = ut. Since we know that u=50m/s, and t=4.285s, this will be easy. s = (50)(4.285) = 214.25 m.

Therefore, horizontal distance reached = 214.25m.

(c) With what velocity will it strike the ground?

In this part, we need to find final velocity. Final velocity = the resultant vector of both the x and y velocity components.
`v=√((v_x)^2+(v_y)^2)`.

Since horizontal velocity is constant, u = v, and therefore, v(x) = 50m/s.

For vertical velocity, we can use
`v^2=u^2-2gs`. u(x) = 0, and s(y) = -90m.

Therefore, v² = -2(9.8)(-90). final vertical velocity is thus 42m/s.

Now final velocity = √(50² + 42²) ≈ 65.3 m/s.

Lastly, we need to remember to calculate direction, since velocity is a vector quantity. the direction of velocity (θ)
`=tan^(-1)((v_y)/(v_x))`

Therefore, θ = 40°.

Therefore, final velocity = 65.3m/s, at 40° downwards.