Question

A simple pendulum of length 5.5 m makes 10.0 complete swings in 25 s what is the acceleration due to gravity at the location of the pendulum ?

Answer 1

The acceleration due to gravity at the location of the pendulum is 34.74 m/s².

Step-by-step explanation:

Given that,

The length of a simple pendulum, l = 5.5 m

It makes 10.0 complete swings in 25 s.

Frequency of pendulum,

`f=(10)/(25)\\\\f=0.4\ Hz`

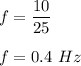
The time period of a simple pendulum is given by :

`T=2\pi \sqrt{(l)/(g)}`

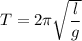
Frequency,

`f=(1)/(T)\\\\f=\frac{1}{2\pi \sqrt{(l)/(g)} }\\\\f=(1)/(2\pi)\sqrt{(g)/(l)}`

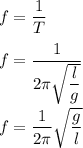
g is the acceleration due to gravity at the location where the pendulum is placed. So,

`f^2=(g)/(4\pi^2l)\\\\g=f^2* 4\pi^2l\\\\g=0.4^2* 4\pi^2* 5.5\\\\g=34.74\ m/s^2`

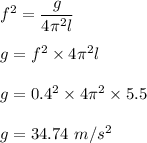
So, the acceleration due to gravity at the location of the pendulum is 34.74 m/s².