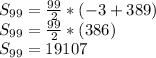Question

Find the sum of the following arithmetic series:

Answer 1

19107

Explanation:

First, we need to find the common difference (d), which we can find by subtracting two consecutive terms. Thus, we can do d = 1 - (-3) = 4.

Now, we need to know how many terms are in the arithmetic series. We can find the number using nth term formula, which is

`a_(n)=a_(1)+(n-1)*d`, where a1 is the first term, n is the term position (e.g., 1st, 2nd).

Although we don't know the term position of 389, we can still plug it into the formula and solving for n will reveal it's term number and the total number of sums in the sequence:

`389=-3+(n-1)*4\\392=(n-1)*4\\392=4n-4\\396=4n\\99=n`

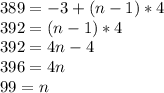
Now, we can find the sum using the sum formula, which is

`S_(n)=n/2*(a_(1)+a_(n))`

Sn can become S99 since there are 99 terms and we can let an = a99, which we know is 389.

Now, we must solve for S99:

`S_(99)=(99)/(2)*(-3+389)\\ S_(99)=(99)/(2)*(386)\\ S_(99)=19107`