Question

Find the measure of CD.
Round to the nearest tenth.
mCD=[?]degrees

Answer 1

m(arc CD) = 14.1 cm

Explanation:

Measure of an arc of the circle =
`(\theta)/(360)(2\pi r)`

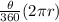
Here 'r' = radius of the circle

θ = Angle subtended by the arc at the center of the circle

From triangle OED,

sin(∠EOD) =
`(ED)/(OD)`

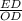
sin(∠EOD) =
`((12.7)/(2))/(9.06)`

=
`(6.35)/(9.06)`

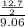
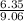
= 0.7

m∠EOD = 44.498

≈ 44.5°

Angle subtended by the arc CD at the center = m∠COD

= 2(44.5)

= 89°

m(arc CD) =
`(89)/(360)(2\pi)(9.06)`

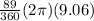
= 14.07

≈ 14.1 cm