Answer:
The roots and x-coordinates of the equation are
 and
and

The vertex of the parabola is

Explanation:
Given

Complete the Square, X intercepts, and Roots

Write
 as a fraction.
as a fraction.


Factor the left hand side.
Write
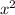 as a fraction with a common denominator, multiply by
as a fraction with a common denominator, multiply by
 .
.

Combine
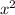 and
and
 .
.

Combine the numerators over the common denominator.

To write
 as a fraction with a common denominator, multiply by
as a fraction with a common denominator, multiply by
 .
.

Combine
 and
and
 .
.

Combine the numerators over the common denominator.

For a polynomial of the form
 , rewrite the middle term as a sum of two terms whose product is
, rewrite the middle term as a sum of two terms whose product is
 and whose sum is
and whose sum is
 .
.

Rewrite 36 as 10 plus 26.

Apply the distributive property.

Group the first two terms and the last two terms.

Factor out the GCF from each group.

Factor the polynomial by factoring out the GCF.

Set the numerator equal to zero.
If any individual factor on the left side of the equation is equal to 0, the entire expression will be equal to 0.

Solving for
 in each equation gives us
in each equation gives us
 and
and

The final solution is

These values of
 are the roots of the equation and lie on the x-axis.
are the roots of the equation and lie on the x-axis.
Vertex
We can use the formula
 to evaluate the vertex.
to evaluate the vertex.
This formula is for a polynomial of the form
 .
.

In this case

Inserting our values into the equation yields

