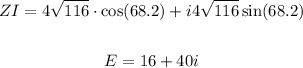We have the following equation to solve
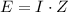
Where E, I, and Z are complex numbers, therefore let's put it in numbers
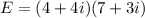
We can solve it directly into the rectangular form by doing the distrutive
Then
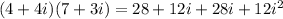
Remember that
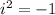
Then
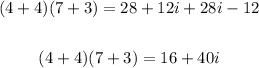
Now we have completely solved the problem!
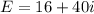
______________________
The second solution (usual)
When we have real engineering problems, we like to do multiplication and division with the polar form, then let's convert Z and I to the polar form
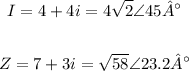
Now to do the multiplication we multiple the magnitude and sum the phases (angles)
![\begin{gathered} ZI=4√(2)\cdot√(58)\angle45°+23.2° \\ \\ ZI=4√(116)\operatorname{\angle}68.2° \end{gathered}]()
We already have the result, now just put it in the rectangular form