Question

Find the coordinates of the missing endpoint if m is the midpoint of ab. a(-9, -4) and m(-7, -2.5)

Answer 1

The coordinates of the point b are:

b(x₂, y₂) = (-5, -1)

Explanation:

Given

As m is the midpoint, so

m(x, y) = m (-7, -2.5)

The other point a is given by

a(x₁, y₁) = a(-9, -4)

To determine

We need to determine the coordinates of the point b

= ?

Using the midpoint formula

`\left(x,\:y\right)=\left((x_2+x_1)/(2),\:\:(y_2+y_1)/(2)\right)`

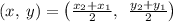
substituting (x, y) = (-7, -2.5), (x₁, y₁) = (-9, -4)

`\left(-7,\:-2.5\right)=\left((x_2+\left(-9\right))/(2),\:\:(y_2+\left(-4\right))/(2)\right)`

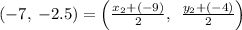
Thus equvating,

Determining the x-coordinate of b

[x₂ + (-9)] / 2 = -7

x₂ + (-9) = -14

x₂ - 9 = -14

adding 9 to both sides

x₂ - 9 + 9 = -14 + 9

x₂ = -5

Determining the y-coordinate of b

[y₂ + (-4)] / 2 = -2.5

y₂ + (-4) = -2.5(2)

y₂ - 4 = -5

adding 4 to both sides

y₂ - 4 + 4 = -5 + 4

y₂ = -1

Therefore, the coordinates of the point b are:

b(x₂, y₂) = (-5, -1)