SOLUTION:
Step 1:
In this question, we are given the following:
Diagram 3 shows a piece of rectangular cardboard and an open box that is made from the cardboard.
The box is made by cutting out four squares of equal size from the corners
of the cardboard then folding up the sides.
Find
a) the length in cm of sides of the squares to be cut out in order to get a box with the largest volume.
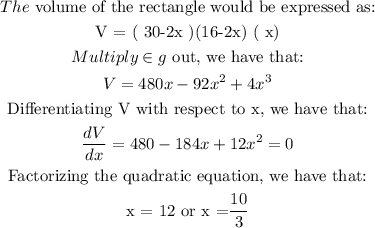
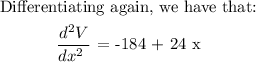
To get the maximum, we need to substitute the values of :
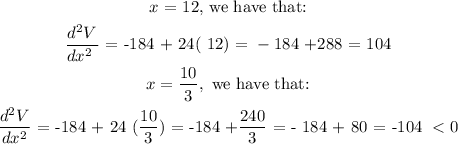
At this stage, we can see that:
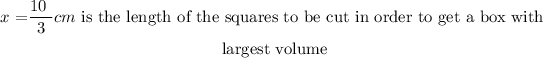
b) Find the minimum number of the boxes needed to fill with 5645 cm³ of pudding

Minimum number of boxes =
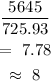
CONCLUSION:
A minimum of 8 boxes will be needed to fill with 5645 cm³ of pudding