Question

Two positive charges are fixed a distance apart.the sun of their charges is Qt.what charge must each have in order to maximise the electric force between them

Answer 1

Both charges must have the same charge, Qt/2.

Step-by-step explanation:

Let the two charges have charge Q1 and Q2, respectively.

Use Coulombs's Law to find an expression for the force between the two charges.

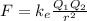`F = k_e(Q_1Q_2)/(r^2)`, where

Ke is Coulomb's contant and

r is the distance between the charges.

We know from the question that

Q1 + Q2 = Qt

So,

Q2 = Qt - Q1

`F = k_e(Q_1(Q_t - Q_1))/(r^2)`

Simplify to obtain,

`F = (k_e)/(r^2) (Q_tQ_1 - Q_1^2)`

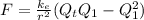
In order to find the value of Q1 for which F is the maximum, we will use the optimization technique of calculus.

Differentiate F with respect to Q1,

`(dF)/(dQ_1) = (k_e)/(r^2) (Q_t - 2Q_1)`

Equate the differential to 0, to obtain the value of Q1 for which F is the maximum.

`(k_e)/(r^2) (Q_t - 2Q_1) = 0\\Q_t - 2Q_1 = 0\\2Q_1 = Q_t\\Q1 = (Q_t)/(2)`

It follows that

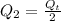`Q_2 = (Q_t)/(2)`.