Answer:
The magnitude of the boat's velocity is 8.21 km/h.
Step-by-step explanation:
We can find the boat's velocity as follows:
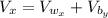
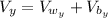
Where:
 and
and
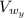 are the components of the velocity of the water in the x and y-direction
are the components of the velocity of the water in the x and y-direction
 and
and
 are the components of the velocity of the boat in the x and y-direction
are the components of the velocity of the boat in the x and y-direction
Since the angle is 15° we have:
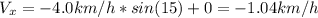
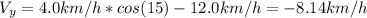
Now, the velocity of the boat is:
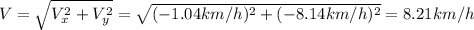
Therefore, the magnitude of the boat's velocity is 8.21 km/h.
I hope it helps you!