Question

Yuri thinks that 3/4 is a root of the following function.

q(x)=6x^3+19x^2-15x-28
Explain to Yuri why 3/4 cannot be a root.

Answer 1

Given:

The polynomial function is

`q(x)=6x^3+19x^2-15x-28`

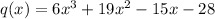
Yuri thinks that
`(3)/(4)` is a root of the given function.

To find:

Why
`(3)/(4)` cannot be a root?

Solution:

We have,

`q(x)=6x^3+19x^2-15x-28`

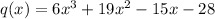
If
`(3)/(4)` is a root, then the value of the function at
`(3)/(4)` is 0.

Putting
`x=(3)/(4)` in the given function, we get

`q((3)/(4))=6((3)/(4))^3+19((3)/(4))^2-15((3)/(4))-28`

`q((3)/(4))=6((27)/(64))+19((9)/(16))-(45)/(4)-28`

`q((3)/(4))=3((27)/(32))+(171)/(16)-(45)/(4)-28`

`q((3)/(4))=(81)/(32)+(171)/(16)-(45)/(4)-28`

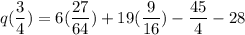
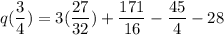
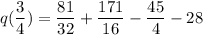
Taking LCM, we get

`q((3)/(4))=(81+342-360-896)/(32)`

`q((3)/(4))=(-833)/(32)\\eq 0`

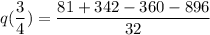
Since the value of the function at
`(3)/(4)` is not equal to 0, therefore,
`(3)/(4)` is not a root of the given function.