Question

What is the solution of the system?
2x+3y=−26
5x+3y=−29

Answer 1

x = -1

y = -8

Explanation:

2x+3y= −26

5x+3y= −29

Time the first equation by -1

-2x - 3y = 26

5x + 3y = -29

3x = -3

x = -1

Now put -1 in for x and solve for y

2(-1) + 3y = - 26

-2 + 3y = -26

3y = -24

y = -8

Let's check

2(-1) + 3(-8) = -26

-2 - 24 = -26

-26 = -26

So, x = -1 and y = -8 is the correct answer.

Answer 2

`2x + 3y = - 26 \\ \implies \: 2x + 3y + 26 = 0`

`5x + 3y = - 29 \\ \implies \: 5x + 3y + 29 = 0`

For finding what sort of solution the pair of equations give , we need to check the type of equality between

`( a_(1))/( a_(2) \: ) , \: ( b_(1) )/( b_(2) ) , \: ( c_(1))/( c_(2) ) \\`

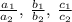
The following results can be obtained ,

`if \: \: ( a_(1) )/(a _(2) ) \\eq \: ( b_(1))/( b_(2)) \\ \\ \implies \: we \: obtain \: a \: unique \: solution`

`if \: \: ( a_(1) )/(a _(2) ) = \: ( b_(1))/( b_(2)) \: \\eq \: ( c_(1))/( c_(2)) \\ \\ \implies \:we \: obtain \: no \: solution`

`if \: \: ( a_(1) )/(a _(2) ) = \: ( b_(1))/( b_(2)) \: = \: ( c_(1))/( c_(2)) \\ \\ \implies \:we \: obtain \: infinitely \: many \: \: solutions`

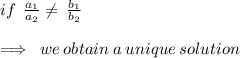
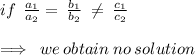
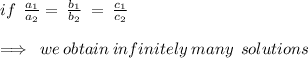
Considering the equations provided ,

`a_(1) = 2 \: \: , \: \: b_(1) = 3 \: \: , \: \: c_(1) = 26 \\ a_(2) = 5 \: \: , \: \: b_(2) = 3 \: \: , \: \: c_(2) = 29`

`\therefore ( a_(1))/( a_(2) ) = (2)/(5) \: \: \: , \: \: \: ( b_(1))/( b_(2) ) = (3)/(3) = (1)/(1) \: \: \: , \: \: \: ( c_(1) )/( c_(2) ) = (26)/(29) \\`

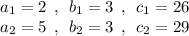
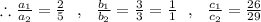
Since ,

`( a_(1) )/( a_(2)) \\eq \: ( b_(1) )/( b_(2)) \\`

The system of equations has a unique solution .

On further calculations done by elimination method , the solution of the equations comes out to be

`\boxed{x = - 1} \\ \boxed{y = - 8}`

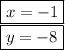
let's have a look at how it'll be done now.

the equations given in the question are -

`2x + 3y + 26 = 0 \: ...(1) \\ 5x + 3y + 29 = 0...(2) \\ \\ multiplying \: equation \: (1) \: by \: - 1 \\ \implies \: - 2x - 3 - 26 = 0...(3) \\ \\ solving \: eqs. \: (2) \: and \: (3) \\ \\ 5x + \cancel{3y} + 29 = 0 \\ \underline{ - 2x \cancel{- 3y} - 26 = 0} \\ 3x + 3 = 0 \\ \\ \implies \: 3x = - 3 \\ \implies \: \boxed{x = - 1}`

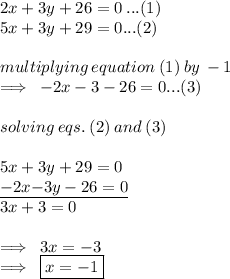
substiting the value of x in equation 1

`2( - 1) + 3y + 26 = 0 \\ 3y + 26 - 2 = 0 \\ 3y + 24 = 0 \\ 3y = - 24 \\ \implies \: \boxed{y = - 8}`

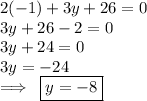
hope helpful! :)