Question

Suppose you make an investment of $1000 that you are not allowed to cash for 50 years. Unfortunately, the value of the investment decreases by 10% per year. How long will it be before your investment decreases to half its original value?

Answer 1

Logarithms

It will decrease to half its original value after 7 years.

Step-by-step explanation

The value of the investment decreases by 10% per year. This means that it will remain at 90% of its previous year's value.

The 90% of any value is found by multiplying the percentage divided by 100:

`(90)/(100)=0.9`

Step 1- writing an equation of the situation

We have that after 1 year the value of the investment will be given by the 90% of $1000. This is:

`1000\cdot0.9`

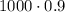
After 2 years, it will be the 90% of the last value:

`1000\cdot0.9\cdot0.9=1000\cdot0.9^2`

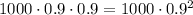
After 3 years, it will be the 90% of the last value:

`1000\cdot0.9^2\cdot0.9=1000\cdot0.9^3`

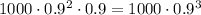
After 4 years, it will be the 90% of the last value:

`1000\cdot0.9^3\cdot0.9=1000\cdot0.9^4`

...

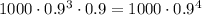
we can see a relation between the exponent of 0.9 and the years that have passed.

After n years, it will be

`1000\cdot0.9^n`

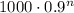
We want to find when the value decreases to half its original value. Since

1000/2 = 500

then, we want to find the number of the year n when the value if 500:

`\begin{gathered} 1000\cdot0.9^n=500 \\ \downarrow \\ n=\text{?} \end{gathered}`

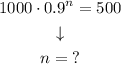
Step 2 - solving the equation for n

In order to find the year when the value is at half the original, we must solve the equation for n.

First, we take 1000 to the right side:

`\begin{gathered} 1000\cdot0.9^n=500 \\ \downarrow\text{ dividing both sides by 1000} \\ (1000\cdot0.9^n)/(1000)=(500)/(1000) \\ 0.9^n=(500)/(1000) \\ \downarrow\text{ since }(500)/(1000)=0.5 \\ 0.9^n=0.5 \end{gathered}`

We want to "leave n alone" on one side of the equation, in order to do it we use logarithm.

Let's remember the relation between logarithms and exponentials:

`b^c=a\rightleftarrows\log _ba=c`

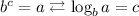
Then, in this case:

`0.9^n=0.5\rightleftarrows\log _(0.9)0.5=n`

Using the calculator, we have:

`\log _(0.9)0.5=6.5788`

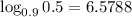
If we round the answer we will have that

`\log _(0.9)0.5=6.5788\approx6.6\approx7`

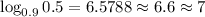
Then, n = 7

Therefore, after 7 years the investment decreases to half its original value.