Given:
The polynomial function is
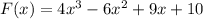
To find:
The possible roots of the given polynomial using rational root theorem.
Solution:
According to the rational root theorem, all the rational roots and in the form of
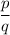 , where, p is a factor of constant and q is the factor of leading coefficient.
, where, p is a factor of constant and q is the factor of leading coefficient.
We have,
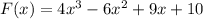
Here, the constant term is 10 and the leading coefficient is 4.
Factors of constant term 10 are ±1, ±2, ±5, ±10.
Factors of leading term 4 are ±1, ±2, ±4.
Using rational root theorem, the possible rational roots are
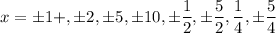
Therefore, the correct options are A, C, D, F.