Question

Solving Equation with Root and Power. Can someone please step by step explain how to solve this problem please?

Answer 1

x = 1

Explanation:

You want to solve for x:

`\sqrt{3+((4+√(x+3))^2)/(6)}=3`

Solution

At any stage where there is a root, you isolate the radical and raise both sides of the equation to a power sufficient to eliminate the radical. Repeat as necessary.

Outer radical

The radical is already on one side of the equation by itself, so we simply square both sides:

`3+((4+√(x+3))^2)/(6)=9\\\\(4+√(x+3))^2=6^2\qquad\text{subtract 3, multiply by 6}\\\\|4+√(x+3)|=6\qquad\text{take the square root}`

Inner radical

At this point, we note that the sum cannot be negative, so the absolute value bars are irrelevant. Isolating the radical and squaring both sides, we can finish the solution.

`4+√(x+3)=6\\\\√(x+3)=2\qquad\text{subtract 4}\\\\x+3=4\qquad\text{square both sides}\\\\\boxed{x=1}\qquad\text{subtract 3}`

This is the only solution, as the attached graph shows.

__

Additional comment

Generally, the square root symbol means the positive square root. That is, √z is usually considered to be non-negative. This is why we use ±√z when we want both signs of the root.

In this problem, the only root we're taking as part of the solution is the root of a square. The possibility of a negative value for the term being squared is handled by using the absolute value brackets: √(z²) = |z|.

For solving these using a graphing calculator, we like to rewrite the equation to the form f(x)=0. That way, the solutions are the x-intercepts.

Answer 2

`x=1`

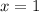
Explanation:

First, square both sides.

`\left(\sqrt{3+(\left(4 + √(x+3) \, \right)^2)/(6)}\, \right)^2= 3^2`

`3+(\left(4 + √(x+3) \, \right)^2)/(6) = 9`

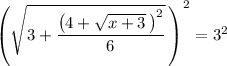
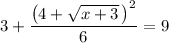
This eliminates the square root over the entire left side of the equation.

Next, multiply both sides by 6 to get rid of the fraction on the left side.

`6\left(3+(\left(4 + √(x+3) \, \right)^2)/(6)\right) = 6( 9)`

`6(3) + \left(4 + √(x+3) \, \right)^2 = 6(9)`

`18 + \left(4 + √(x+3) \, \right)^2 = 54`

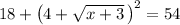
Then, subtract 18 from both sides to isolate the squared term.

`18 + \left(4 + √(x+3) \, \right)^2 = 54\\\underline{-18 \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \: } \ \ \ \ \ \underline{ - 18}`

`\left(4 + √(x+3) \, \right)^2 = 36`

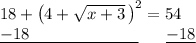
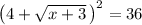
Now, we can square root both sides.

`\sqrt{\left(4 + √(x+3) \, \right)^2} = √(36)`

`4 + √(x+3) = \pm 6`

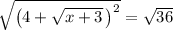
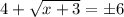
Remember to use apply the even root property, so that the right side (6) is positive or negative (indicated by the plus or minus sign).

Next, subtract 4 from both sides.

`4 + √(x+3) = \pm 6 \\ \underline{-4\ \ \ \ \ \ \ \ \ \ \: } \ \ \ \ \ \underline{ - 4}`

`√(x+3) = \pm 6 - 4`

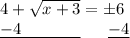
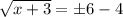
Then, square both sides to get rid of the square root on the left side.

`\left(√(x+3)\right)^2 = (\pm 6 - 4)^2`

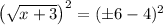
`x+3 = 2^2` OR
`x+3 = (-10)^2`

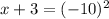
We can see that there are two resulting expressions, each of which we can solve individually.

`x+3 = 4` OR
`x+3 = 100`

`\boxed{x = 1}`
`\boxed{x\\e97}`

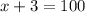
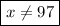
The reason that x = 97 is crossed out is because when we plug that x-value back into the original equation, it does not come out to be true. Therefore, 97 is an extraneous solution.

Also, see the attached image for another solution (that implores another method).