Question

Please please I need help asap on this !

Answer 1

Explanation:

It is given that ,

tanA=3/4 ,
`\pi < A < (3\pi )/(2)`

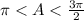
so , angle are in 3rd Quadrant .

cosB = -15/17 ,
`(\pi)/(2) < B < \pi`

So, angle B are in 2nd Quadrant

We use Compound formula of tan(A+B)

`tan(A+B) = (tanA + tanB)/(1- tanAtanB)` ..........(1)

To use this formula , we need to find the value of tanA and tanB.

tanA = 3/4 ........ given

cos B =-15/17

Using Identity ,

`sin^(2)B + cos^(2)B=1`

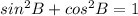
put the value of cosB

`sin^(2)B + (-(15)/(17))=1\\ sin^(2)B = 1 - (225)/(289) \\sin^(2)B = (64)/(289) \\sinB = (8)/(17)`

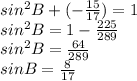
we know that ,

tanB = sinB/cosB

put the value of sinB and CosB

`tanB = ((8)/(17) )/(-(15)/(17)) \\tanB = - (8)/(15)`

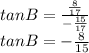
`tanB = -(-(8)/(15)) \\tanB = (8)/(15)`the value of tan in 2nd quadrant are negative .

We find the value of tanB and next we put the value of tanA and tanB in

equation(1)

`tan(A+B) = (tanA + tanB)/(1- tanAtanB)\\tan(A+B) = ((3)/(4)+(8)/(15))/(1 - (3)/(4)(8)/(15) ) \\tan(A+B) = ((77)/(60) )/(1 - (24)/(60) ) \\tan(A+B) = ((77)/(60) )/((36)/(60) ) }\\tan(A+B) = (77)/(36)`

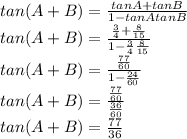
Hopeful,this answer will help you!

If any wrong in this answer please let me know