Question

Josh is at a park. He knows that the distance from the picnic table to a tree is 124 feet. Josh also knows the angle formed by a segment from his location to the picnic table and a segment from his position to the tree is 54 degrees and that triangle formed by his position, the picnic table, and the tree is a right triangle, with a right angle at the picnic table. Does josh have enough to find how far he is from the picnic table.

Answer 1

Yes, Josh has enough information to find how far he is from the picnic table. Josh is 90.1 ft from the picnic table (to the nearest tenth).

Explanation:

Yes, Josh has enough information to find how far he is from the picnic table.

From the given information, we can model this as a right triangle where the angle is 54°, the side opposite the angle is the distance between the picnic table and the tree, and the side adjacent the angle is the distance between Josh and the picnic table. (See attached diagram).

To calculate the distance between Josh and the picnic table (labelled "x" on the attached diagram), use the tangent trigonometric ratio.

`\boxed{\begin{minipage}{6 cm}\underline{Tangent trigonometric ratio} \\\\$\sf \tan(\theta)=(O)/(A)$\\\\where:\\ \phantom{ww}$\bullet$ $\theta$ is the angle. \\ \phantom{ww}$\bullet$ $\sf O$ is the side opposite the angle. \\\phantom{ww}$\bullet$ $\sf A$ is the side adjacent the angle. \\\end{minipage}}`

Substitute the values into the tan ratio:

`\implies \tan 54^(\circ)=(124)/(x)`

`\implies x=(124)/(\tan 54^(\circ))`

`\implies x=90.09127...`

`\implies x=90.1\; \sf ft\;(nearest\;tenth)`

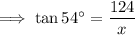
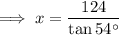
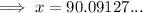
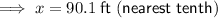
Therefore, Josh is 90.1 ft from the picnic table (to the nearest tenth).