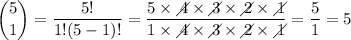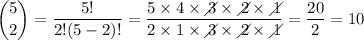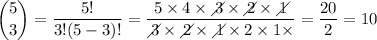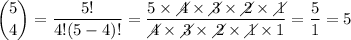Question

use the binomial theorem to write down and simplify all the terms of the expansion (1 - 1/4 x) raised to 5 ​

Answer 1

`\displaystyle 1-(5)/(4)x+(5)/(8)x^2-(5)/(32)x^3+(5)/(256)x^4-(1)/(1024)x^5`

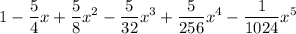
Explanation:

A binomial expansion is the result of multiplying out the brackets of a polynomial with two terms.

Use the binomial formula to expand the given expression.

Binomial series formula

`\displaystyle \left(1+ax\right)^n=1+\binom{n}{1}(ax)+\binom{n}{2}(ax)^2+\binom{n}{3}(ax)^3+...+(ax)^n`

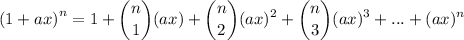
where:

`\displaystyle \binom{n}{r}=(n!)/(r!(n-r)!)=\phantom{l}^nC_r`

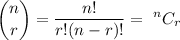
Given expression:

`\left(1-(1)/(4)x\right)^5`

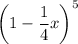
Therefore:

• a = -1/4
• n = 5

Substitute a = -1/4 and n = 5 into the binomial formula:

`\displaystyle =1+\binom{5}{1}\left(-(1)/(4)x\right)+\binom{5}{2}\left(-(1)/(4)x\right)^2+\binom{5}{3}\left(-(1)/(4)x\right)^3+\binom{5}{4}\left(-(1)/(4)x\right)^4+\left(-(1)/(4)x\right)^5`

`\displaystyle =1+5\left(-(1)/(4)x\right)+10\left((1)/(16)x^2\right)+10\left(-(1)/(64)x^3\right)+5\left((1)/(256)x^4\right)+\left(-(1)/(1024)x^5\right)`

`\displaystyle =1-(5)/(4)x+(10)/(16)x^2-(10)/(64)x^3+(5)/(256)x^4-(1)/(1024)x^5`

`\displaystyle =1-(5)/(4)x+(5)/(8)x^2-(5)/(32)x^3+(5)/(256)x^4-(1)/(1024)x^5`

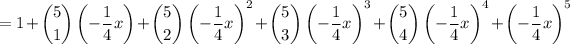
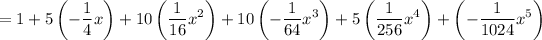
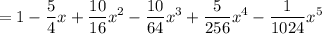
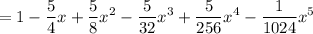
Therefore, the expansion of (1 - ¹/₄x)⁵ is:

`\displaystyle \left(1-(1)/(4)x\right)^5=1-(5)/(4)x+(5)/(8)x^2-(5)/(32)x^3+(5)/(256)x^4-(1)/(1024)x^5`

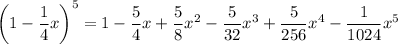
Please note there was note enough room to add the binomial coefficients calculations to the main calculation, so please find them below:

`\displaystyle \binom{5}{1}=(5!)/(1!(5-1)!)=(5* \diagup\!\!\!\!4*\diagup\!\!\!\!3*\diagup\!\!\!\!2*\diagup\!\!\!\!1)/(1*\diagup\!\!\!\!4*\diagup\!\!\!\!3*\diagup\!\!\!\!2*\diagup\!\!\!\!1)=(5)/(1)=5`

`\displaystyle \binom{5}{2}=(5!)/(2!(5-2)!)=(5* 4*\diagup\!\!\!\!3*\diagup\!\!\!\!2*\diagup\!\!\!\!1)/(2 * 1* \diagup\!\!\!\!3*\diagup\!\!\!\!2*\diagup\!\!\!\!1)=(20)/(2)=10`

`\displaystyle \binom{5}{3}=(5!)/(3!(5-3)!)=(5* 4*\diagup\!\!\!\!3*\diagup\!\!\!\!2*\diagup\!\!\!\!1)/(\diagup\!\!\!\!3*\diagup\!\!\!\!2*\diagup\!\!\!\!1*2 * 1*)=(20)/(2)=10`

`\displaystyle \binom{5}{4}=(5!)/(4!(5-4)!)=(5* \diagup\!\!\!\!4*\diagup\!\!\!\!3*\diagup\!\!\!\!2*\diagup\!\!\!\!1)/(\diagup\!\!\!\!4*\diagup\!\!\!\!3*\diagup\!\!\!\!2*\diagup\!\!\!\!1 * 1)=(5)/(1)=5`