Question

100 Points. Please Help. Due in Two Hours.

Answer 1

`2 {x}^(2) - 4x - 3 = 0`

A Here ,

`\boxed{a = 2 }\\\boxed{b = - 4} \\ \boxed{c = - 3}`

B Filling in the values of a , b and c in the Quadratic formula below , we get

`x = \frac{- (b)\pm \sqrt{( {b}^(2)) - 4(a)(c) } }{2(a)} \\`

C Simplifying each section , we get

`x = \frac{ - ( - 4) + \sqrt{( { - 4}^(2) ) - 4(2)( - 3)} }{2 * 2}`

or

`x = \frac{ - ( - 4) - \sqrt{ {( - 4})^(2) - 4(2)( - 3) } }{2 * 2}`

D Simplifying answers from Part C , we get

`\boxed{x = (2 + √(10) )/(2)} \: \: \: \: or \: \: \: \: \boxed{ x = (2 - √(10) )/(2) } \\`

Therefore ,

`\boxed{x = 2.58} \: \: \: \: and \: \: \: \: \boxed{x = - 0.58}`

Thus , option A. is correct!

_____________________________________

`{x}^(2) + 2x = 1 \\ \implies \: {x}^(2) + 2x - 1 = 0`

A Here ,

`\boxed{a = 1} \\ \boxed{b = 2} \\ \boxed{c = - 1}`

B Filling in the values of a , b and c in the Quadratic formula below , we get

`x = \frac{- (b)\pm \sqrt{( {b}^(2)) - 4(a)(c) } }{2(a)} \\`

C Simplifying each section , we get

`x = \frac{ - (2) + \sqrt{ ({2}^(2) ) - 4(1)( - 1)} }{2 * 1}`

or

`x = \frac{ - (2) - \sqrt{( {2}^(2)) - 4(1)( - 1) } }{2 * 1}`

D Simplifying answers from Part C , we get

`\boxed{x = - 1 + √(2) } \: \: \: \: or \: \: \: \: \boxed{x = - 1 - √(2) }`

Therefore

`\boxed{x = 0.41} \: \: \: \: or \: \: \: \: \boxed{x = -2.41 }`

Thus , option D is correct.

hope helpful! :)

Answer 2

2. The given quadratic equation is in the general form:

ax² + bx + c = 0

therefore:

a = 2

b = -4

c = -3

The quadratic formula is thus:

`x=(-b(+-)√(b^2-4ac) )/(2a)`

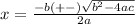
Substituting the values found for a, b, and c:

`x=(-(-4)+√((-4)^2-4(2)(-3)) )/(2(2))` and
`x=(-(-4)-√((-4)^2-4(2)(-3)) )/(2(2))`

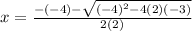
Therefore x = 2.58, x = -0.58

3. Using the same method as above, first, bring all values to one side, leaving the RHS = 0

a = 1

b = 2

c = -1

The quadratic formula is thus:

`x=(-b(+-)√(b^2-4ac) )/(2a)`

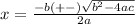
Substituting the values found for a, b, and c:

`x=(-(2)+√((2)^2-4(1)(-1)) )/(2(1))` and
`x=(-(2)-√((2)^2-4(1)(-1)) )/(2(1))`

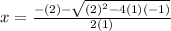
Therefore, x = 0.41, x = -2.41