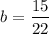Answer:

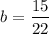
Explanation:
To find the equation of the tangent line to the curve
 at the point
at the point
 we need to first find the derivative of the equation with respect to x using implicit differentiation.
we need to first find the derivative of the equation with respect to x using implicit differentiation.
Taking the derivative of both sides with respect to x:
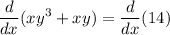
Using the product rule and chain rule:
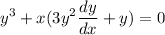
Simplifying and solving for
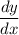
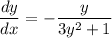
Now we can substitute x=7 and y=1 into this equation to find the slope of the tangent line at the point (7,1):
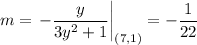
So the slope of the tangent line is
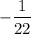
To find the y-intercept, we can use the point-slope form of the equation of a line:
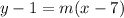
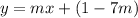
Therefore, the equation of the tangent line to the curve
 at the point (7,1) can be written as:
at the point (7,1) can be written as:
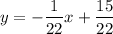
So
 and
and