Question

3. A prop for the theater club’s play is constructed as a cone topped with a half-sphere. What is the volume of the prop? Round your answer to the nearest tenth of a cubic inch. Use 3.14 to approximate pi.

Answer 1

Given:-

• A prop for threatre is constructed using a cone and a hemisphere.
• Use π = 3.14

To find:-

• The volume of the prop .

Answer:-

The given figure is made up of a cone and a hemisphere , so to find the total volume , we would find the volume of cone and hemisphere individually and add them up to find the net volume.

Finding volume of cone:

The data we have is ,

• Height = 14inches
• Radius = 9inches .

As we know that the volume of cone is given by,

`\implies V =(1)/(3)\pi r^2 h \\`

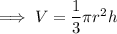
on substituting the respective values,we have;

`\implies V =(1)/(3)* 3.14 * (9in.)^2 * 14in .\\`

`\implies V = (1)/(3)* 3.14 * 81in.^2* 14in. \\`

`\implies V = 1186.92 \ in.^3 \\`

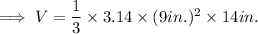
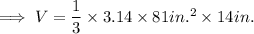
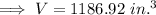
Finding the volume of hemisphere:

As we know that the volume of hemisphere is given by;

`\implies V =(2)/(3)\pi r^3 \\`

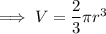
And here ,

• r = 9 inches .

So that;

`\implies V =(2)/(3)* 3.14* (9\ in.)^3 \\`

`\implies V =(2)/(3)* 3.14* 729\ in.^3 \\`

`\implies V = 1526.04 \ in.^3 \\`

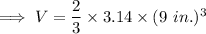
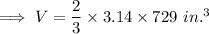
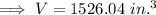
Hence the total volume will be ,

`\implies V_(prop) = (1526.04 + 1186.92 )in.^3\\`

`\implies V = 2712.96 \ in.^3 \\`

`\implies \underline{\underline{ V_(prop)= 2713\ in.^3 }} \\`

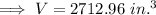
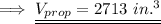
Hence the volume of prop is 2713 in.³

and we are done!

Answer 2

2713.0 in³ (nearest tenth)

Explanation:

To calculate the volume of the prop, sum the volume of the cone and the volume of the half-sphere.

`\boxed{\begin{minipage}{4 cm}\underline{Volume of a cone}\\\\$V=(1)/(3) \pi r^2 h$\\\\where:\\ \phantom{ww}$\bullet$ $r$ is the radius. \\ \phantom{ww}$\bullet$ $h$ is the height.\\\end{minipage}}`
`\boxed{\begin{minipage}{4 cm}\underline{Volume of a half-sphere}\\\\$V=(2)/(3) \pi r^3$ \\\\ where:\\ \phantom{ww}$\bullet$ $r$ is the radius. \\\end{minipage}}`

Therefore, the equation for the volume of the prop is:

`V_(\sf prop)=(1)/(3) \pi r^2 h+(2)/(3) \pi r^3`

From inspection of the given diagram:

• r = 9 in
• h = 14 in
• π ≈ 3.14

Substitute the values of r, h and π into the equation and solve for V:

`\begin{aligned}\implies V_(\sf prop)&=(1)/(3) \pi r^2 h+(2)/(3) \pi r^3\\\\&=(1)/(3) (9)^2 (14)+(2)/(3) \pi (9)^3\\\\ &=(1)/(3) \pi (81) (14)+(2)/(3) \pi (729)\\\\ &=378 \pi+486 \pi\\\\ &=864 \pi\\\\&=864 \cdot 3.14\\\\&=2712.96\\\\&=2713.0\;\sf in^3\;\;(nearest\;tenth)\end{aligned}`

Therefore, the volume of the prop is 2,713.0 in³ to the nearest tenth.