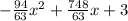Explanation:
I am going to assume this is a quadratic so
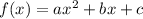
When 3 is c
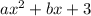
When x is 7,
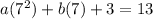
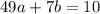
When x is 9,
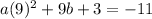
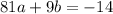
We have two system, let's eliminate the b variable by multiplying the second system by
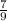
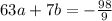
Bring down the first system
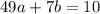
Subtract the two system,
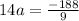
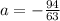
Plugging in a, we will eventually get

So our quadratic is