Question

As seen in the diagram below, Austin is building a walkway with a width of xx feet to go around a swimming pool that measures 8 feet by 10 feet. If the total area of the pool and the walkway will be 360 square feet, how wide should the walkway be?

Answer 1

We can start the problem by using the formula for the area of a rectangle:Area = length x widthThe total area of the pool and the walkway is given as 360 square feet. Let's assume that the width of the walkway is w feet. Then, the dimensions of the entire area can be represented as (8 + 2w) by (10 + 2w) feet, since there is an additional width of w feet on both sides of the pool. Therefore, we can set up the equation:(8 + 2w) x (10 + 2w) = 360 Expanding the left side and simplifying, we get:4w^2 + 36w - 80 = 0We can solve for w using the quadratic formula:w = (-b ± sqrt(b^2 - 4ac)) / 2aIn this case, a = 4, b = 36, and c = -80. Substituting these values into the formula, we get:w = (-36 ± sqrt(36^2 - 4(4)(-80))) / 8w = (-36 ± sqrt(1872)) / 8w ≈ -5.6 or w ≈ 3.6Since the width cannot be negative, we can discard the first solution. Therefore, the width of the walkway should be approximately 3.6 feet.

Explanation:

Answer 2

To achieve a total area of 360 square feet for the pool and walkway, the width of the walkway (xx feet) should be 7 feet.

The total area of the pool and walkway can be expressed as the sum of two rectangular areas: the pool and the walkway. The dimensions of the pool are given as 8 feet by 10 feet. Assuming the walkway width is xx feet, the dimensions of the outer rectangle (pool + walkway) become (8 + 2xx) by (10 + 2xx). The formula for the total area (A) is
`\(A = \text{length} * \text{width}\).`

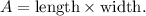
Setting the total area equal to 360 square feet and substituting the dimensions, we get the equation:

`\[ (8 + 2xx) * (10 + 2xx) = 360.\]`

Solving for xx involves simplifying the equation and finding the value that satisfies it. After solving, we find that xx is equal to 7 feet. Therefore, the walkway should be 7 feet wide to achieve a total area of 360 square feet.

Understanding the relationship between dimensions, areas, and the desired total area is crucial for solving problems involving geometric figures. In this scenario, the equation represents the relationship between the pool dimensions, walkway width, and the specified total area. The solution, xx = 7 feet, ensures that the combined area of the pool and walkway meets the given requirement of 360 square feet.