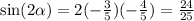Question

I need help with number 1 the tan= 4/3, lies in quadrant ||| Find sin20

It’s due tonight at 11:59 and I’m struggling

Answer 1

Explanation:

Step 1: Simplify the identity we need to find

`\sin(2x) = 2 \sin(x) \cos(x)`

So we need to find sin and cos

Here, we are given tan(x)

A simple way to find sin (x) and cos(x) when given tan(x) is to use the definition of the trig functions of acute angles.

`\tan( \alpha ) = (y)/(x)`

`\cos( \alpha ) = (x)/(r)`

`\sin( \alpha ) = (y)/(r)`

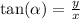
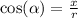
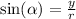
where r is

`r = \sqrt{ {x}^(2) + {y}^(2) }`

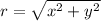
Here, y is 4 and x is 3.

So

`r = \sqrt{ {3}^(2) + {4}^(2) } = 5`

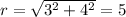
Since both cosine and sine are in quadrant 3, they are both negative.

Know we can plug in the knowns, since we know x,y, and r.

`\cos( \alpha ) = - (3)/(5)`

`\sin( \alpha ) = - (4)/(5)`

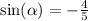
Now plug in the knowns for sin 2a

`\sin(2 \alpha ) = 2( - (3)/(5) )( - (4)/(5) ) = (24)/(25)`