Question

2x − 6y = 12

−x + 3y = 1
For the following exercises, determine whether the lines given by the equations below are parallel, perpendicular, or neither parallel nor perpendicular:

Answer 1

We are given the following set of equations,

`2x-6y=12 \\ -x+3y=1`

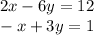
and asked to determine whether they are parallel, perpendicular or neither. We first need to alter each equation and put into slope-intercept form,
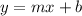`y=mx+b` (m=slope/rate of change, b=y-intercept). Then we can follow the following basic guidelines,

`\Rrightarrow` Lines that are parallel will have slopes that are equal (
`m =m`) .

`\Rrightarrow` Lines that are perpendicular will have slopes that are reciprocal, opposite signs (
`m \rightarrow -(1)/(m)`).

`\Rrightarrow` Lines that are neither will have slopes that are NOT equal (
`m_(1) \\eq m_(2)`).

Taking the first equation,
`2x-6y=12`, and putting it in slope-int form.

`\Longrightarrow2x-6y=12`

`\Longrightarrow-6y=12-2x`

`\Longrightarrow y=(12)/(-6) -(2)/(-6) x`

`\Longrightarrow y=-2+(1)/(3) x`

`\Longrightarrow y=(1)/(3) x -2`

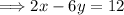
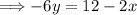
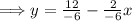
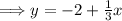
The slope of line 1 is
`(1)/(3)`.

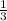Now taking the second equation,
`-x+3y=1`, and putting it in slope-int form.

`\Longrightarrow -x+3y=1`

`\Longrightarrow 3y=1+x`

`\Longrightarrow y=(1)/(3) +(x)/(3)`

`\Longrightarrow y=(1)/(3)x +(1)/(3)`

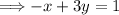
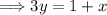
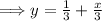
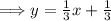
The slope of line 2 is
`(1)/(3)`.

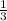Since the slopes of each line are equal, than the lines are parallel.