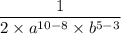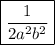Question

Simplifying a Multiplication and Division Algebraic Fraction.

Answer 1

`(1)/(2 a^(2)b^2)`

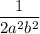
Explanation:

First, we can rewrite the operation unto the third fraction because dividing by a fraction is the same as multiplying by its reciprocal. For example,

`3 / 3 = 3 * (1)/(3) = 1`

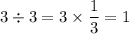
Applying this to the third term:

`(√(a^3b^2))/(6a^3) * (3a^5b)/((a^3b^2)^2) * (√(a^3b^2))/(ab)`

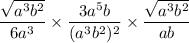
We can now simplify the exponents as well as the square-rooted numbers by distributing an exponent of 1/2.

`(a^(3/2)b^(2/2))/(6a^3) * (3a^5b)/(a^6b^4) * (a^(3/2)b^(2/2))/(ab)`

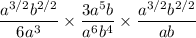
Then, we can combine like terms in the numerators and denominators.

(Remember that
`a^b * a^c = a^(b+c)`)

`(3 * a^([5 \, + \, 2(3/2)]) * b^([1 \, + 1 + 1]))/(6 * a^([3 \, +\, 6\, +\, 1]) * b^([4\, + \, 1]))`

The exponents present can now be simplified.

`(3 * a^8 * b^3)/(6 * a^(10) * b^5)`

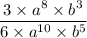
Finally, we can cancel like terms on the top and bottom to simplify completely. (Remember that
`a^b / a^c = a^(b-c)`)

`(1)/(2 * a^(10-8) * b^(5-3))`

`\boxed{(1)/(2 a^(2) b^2)}`