We have to find θ, where:
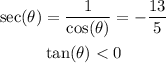
We can transform the first equation as:
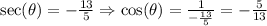
As the tangent of the angle is negative, and the tangent is:
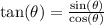
the sine of the angle has to be positive (a quotient between a positive and a negative number is negative).
Then, if the sine is positive and the cosine is negative, then theta is in the second quadrant, between 90° and 180°.
We then can calculate the angle as:
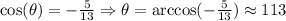
Answer: θ is approximately 113°, located in the second quadrant.