This equation is true for all
 because it simplifies to
because it simplifies to
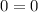 , meaning the value inside the box that makes the equation true is 2.
, meaning the value inside the box that makes the equation true is 2.
The equation presented is:
![\[ x - 2 = -(\Box - x) \]](https://img.qammunity.org/2022/formulas/mathematics/college/7phbjyg7gvq1i991kfz1bwo3k68pqhhokb.png)
To solve for the value in the box
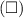 , we need to recognize that the expression inside the parentheses on the right side of the equation will be the opposite sign of
, we need to recognize that the expression inside the parentheses on the right side of the equation will be the opposite sign of
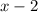 when the negative sign outside the parentheses is distributed.
when the negative sign outside the parentheses is distributed.
Here are the steps to find the value in the box:
1. Identify the Expression: Recognize that
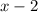 is the expression we are considering.
is the expression we are considering.
2. Apply the Negative Sign*: The negative sign outside of the parentheses will change the sign of both terms inside the parentheses.
3. Match the Expressions: The expression inside the parentheses, once negated, should match
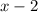 . Since distributing the negative sign across
. Since distributing the negative sign across
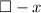 will change the sign of
will change the sign of
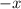 to
to
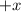 , we want the expression
, we want the expression
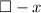 to become
to become
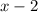 when negated.
when negated.
4. **Solve for the Box**: Knowing that the negative of
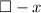 should be
should be
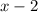 , set
, set

![\[ -\Box + x = x - 2 \]](https://img.qammunity.org/2022/formulas/mathematics/college/vy819fp6vtzzc74n03ne9cpjp7ozu836le.png)
Since
 is on both sides, we can simplify by removing
is on both sides, we can simplify by removing
 from each side:
from each side:
![\[ -\Box = -2 \]](https://img.qammunity.org/2022/formulas/mathematics/college/y8a900iqlgr1mtgiwivnqakcdy1yfnvw3l.png)
![\[ \Box = 2 \]](https://img.qammunity.org/2022/formulas/mathematics/college/w88e1g4wpe8dntieqicwfhf68rxipjias2.png)
The value in the box is 2. This means that the original equation should read:
![\[ x - 2 = -(2 - x) \]](https://img.qammunity.org/2022/formulas/mathematics/college/kbbzppp0axuwcjxyyt4mj77q9dzaxpi1ni.png)
And when you distribute the negative sign inside the parentheses:
![\[ x - 2 = -2 + x \]](https://img.qammunity.org/2022/formulas/mathematics/college/g1l5vnvrbkj1kmq2hq7o01ztj1g13nw1r8.png)
This equation is true for all
 because it simplifies to
because it simplifies to
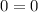 , meaning the value inside the box that makes the equation true is 2.
, meaning the value inside the box that makes the equation true is 2.