Question

Please help me pleasee answer this correctly ​

Answer 1

(a) center = (0, 0)

(b) vertices = (0, ±3)

(c) co-vertices = (±2, 0)

(d) foci = (0, ±√5)

(e) major axis = 6 units

(f) minor axis = 4 units

(g) LR = 8/3 units

Explanation:

`\boxed{\begin{minipage}{6 cm}\underline{General equation of an ellipse}\\\\$((x-h)^2)/(a^2)+((y-k)^2)/(b^2)=1$\\\\where:\\\phantom{ww}$\bullet$ $(h,k)$ is the center\\\end{minipage}}`

Given equation:

`9x^2+4y^2=36`

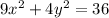
Divide both sides of the equation by 36 to rewrite the given equation in the general equation of an ellipse (so that the right side of the equation is 1):

`\implies (9x^2)/(36)+(4y^2)/(36)=(36)/(36)`

`\implies (\diagup\!\!\!\!9x^2)/(4 \cdot \diagup\!\!\!\!9)+(\diagup\!\!\!\!4y^2)/(\diagup\!\!\!\!4 \cdot 9)=1`

`\implies (x^2)/(4)+(y^2)/(9)=1`

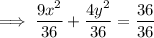
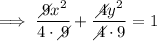
Comparing the equation with the general equation, we can say that:

• h = 0
• k = 0
• a² = 4 ⇒ a = 2
• b² = 9 ⇒ b = 3

Therefore, the center (h, k) of the ellipse is (0, 0).

As b > a, the ellipse is vertical. Therefore:

• b is the major radius and 2b is the major axis.
• a is the minor radius and 2a is the minor axis.
• Vertices = (h, k±b)
• Co-vertices = (h±a, k)
• Foci = (k, h±c) where c² = b² - a²

To find the vertices, substitute the value of b into the formula for the vertices:

`\begin{aligned} \implies (h, k \pm b)&=(0, 0\pm 3)\\&=(0, \pm3)\end{aligned}`

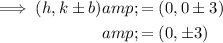
Therefore, the vertices are (0, ±3).

To find the co-vertices, substitute the value of a into the formula for the co-vertices:

`\begin{aligned} \implies (h \pm a, k)&=(0 \pm 2, 0)\\&=(\pm 2,0)\end{aligned}`

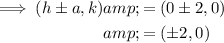
Therefore, the co-vertices are (±2, 0).

To find the value of c, substitute the found values of a and b into c² = b² - a²:

`\begin{aligned}\implies c^2&=b^2-a^2\\c^2&=3^2-2^2\\c^2&=9-4\\c^2&=5\\c&=√(5)\end{aligned}`

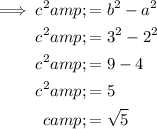
To find the foci, substitute the value of c into the formula for the foci:

`\begin{aligned} \implies (k, h \pm c)&=(0, 0\pm √(5))\\&=(0, \pm √(5))\end{aligned}`

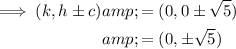
Therefore, the foci are (0, ±√5).

The major axis is 2b:

`\implies 2b=2(3)=6\;\sf units`

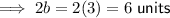
The minor axis is 2a:

`\implies 2a=2(2)=4\;\sf units`

The latus rectum (LR) of an ellipse is a line drawn perpendicular to the its major axis that passes through the foci.

The formula for the endpoints of the latus rectum of a vertical ellipse is:

`\left(h\pm(a^2)/(b), k\pm c \right)`

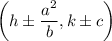
Therefore, substituting the values of h, k, a, b and c into the formula, the coordinates of the latera recta are:

`\implies \left(0\pm(2^2)/(3), 0\pm √(5)\right)`

`\implies \left(\pm(4)/(3), \pm √(5)\right)`

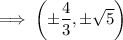
To calculate the length of the latus rectum, subtract the negative x-value from the positive x-value of the endpoints:

`\implies (4)/(3)-\left(-(4)/(3)\right)=(8)/(3)\; \sf units`

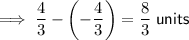
Therefore, the length of the latus rectum is 8/3 units.