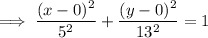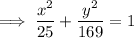Question

Please help me pleasee answer this correctly ​

Answer 1

`\textsf{1)} \quad (x^2)/(169)+(y^2)/(144)=1`

`\textsf{2)} \quad (x^2)/(25)+(y^2)/(169)=1`

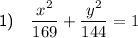
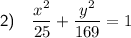
Explanation:

`\boxed{\begin{minipage}{6 cm}\underline{General equation of an ellipse}\\\\$((x-h)^2)/(a^2)+((y-k)^2)/(b^2)=1$\\\\where:\\\phantom{ww}$\bullet$ $(h,k)$ is the center\\\end{minipage}}`

If a > b, the ellipse is horizontal:

• a is the major radius and 2a is the major axis.
• b is the minor radius and 2b is the minor axis.
• Vertices = (h±a, k)
• Co-vertices = (h, k±b)
• Foci = (h±c, k) where c² = a² - b²

If b > a, the ellipse is vertical:

• b is the major radius and 2b is the major axis.
• a is the minor radius and 2a is the minor axis.
• Vertices = (h, k±b)
• Co-vertices = (h±a, k)
• Foci = (k, h±c) where c² = b² - a²

Question 1

Given the center of the ellipse is (0, 0):

• h = 0
• k = 0

Given the vertices are (±13, 0), the ellipse is horizontal.

Equate the vertex formula with the actual vertex and solve for a:

`\begin{aligned}\implies (h \pm a, k) &= (\pm 13, 0)\\(0 \pm a, 0) &= (\pm 13, 0)\\(\pm a, 0) &= (\pm 13, 0)\\a&=13\end{aligned}`

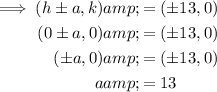
Given the foci are (±5, 0) and the ellipse is horizontal.

Equate the foci formula with the actual foci and solve for c:

`\begin{aligned}\implies (h \pm c, k) &= (\pm 5, 0)\\(0 \pm c, 0) &= (\pm 5, 0)\\(\pm c, 0) &= (\pm 5, 0)\\c&=5\end{aligned}`

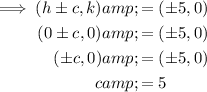
To find b, substitute the found values of a and c into c² = a² − b²:

`\begin{aligned} \implies c^2&=a^2-b^2\\5^2 &= 13^2 - b^2\\b^2 &= 13^2 - 5^2\\b^2 &= 169 - 25\\b^2 &= 144\\b&=12\end{aligned}`

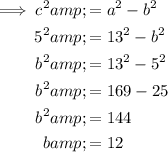
To create an equation of the ellipse with the given properties, substitute the values of h, k, a and b into the general equation of an ellipse:

`\implies ((x-0)^2)/(13^2)+((y-0)^2)/(12^2)=1`

`\implies (x^2)/(169)+(y^2)/(144)=1`

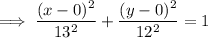
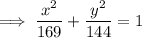
Question 2

Given the foci are (0, ±12), the ellipse is vertical.

Equate the foci formula with the actual foci:

`\begin{aligned}\implies (k, h \pm c) &= (0,\pm 12)\end{aligned}`

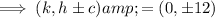
Therefore, the center is (0, 0) and c = 12:

• h = 0
• k = 0
• c = 12

The major axis of a vertical ellipse is 2b.

Given the major axis length is 26 units:

`\begin{aligned}\implies 2b&=26\\b&=13\end{aligned}`

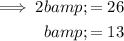
To find a, substitute the found values of b and c into c² = b² - a²:

`\begin{aligned} \implies c^2&=b^2-a^2\\12^2 &=13^2-a^2\\a^2&=13^2 + 12^2\\a^2&=169+144\\a^2&=25\\a&=5\end{aligned}`

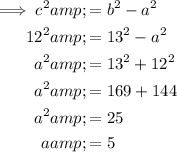
To create an equation of the ellipse with the given properties, substitute the values of h, k, a and b into the general equation of an ellipse:

`\implies ((x-0)^2)/(5^2)+((y-0)^2)/(13^2)=1`

`\implies (x^2)/(25)+(y^2)/(169)=1`