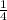Answer:
a₁₅ =
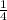
Explanation:
the nth term of a geometric sequence is
 = a₁
= a₁
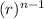
where a₁ is the first term and r the common ratio
we require to fid a₁ and r
given a₄ = - 512 and a₉ = 16 , then
a₁ r³ = - 512 → (1)
a₁
 = 16 → (2)
= 16 → (2)
divide (2) by (1)
 =
=
 ( cancel a₁ on numerator/ denominator on left side )
( cancel a₁ on numerator/ denominator on left side )
 = -
= -
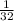
 = -
= -
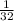
r =
![\sqrt[5]{-(1)/(32) }](https://img.qammunity.org/2024/formulas/mathematics/college/3qqta0tnc46bkk71vy863g625e2av3yqax.png) = -
= -

substitute r = -
 into (1) and solve for a₁
into (1) and solve for a₁
a₁ × (-
 )³ = - 512
)³ = - 512
a₁ × -
 = - 512 ( multiply both sides by - 8 to clear the fraction )
= - 512 ( multiply both sides by - 8 to clear the fraction )
a₁ = 4096
Then
a₁₅ = 4096 ×
 = 4096 ×
= 4096 ×
 =
=
 =
=