ANSWER
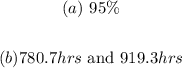
Step-by-step explanation
(a) Given that:
Mean, μ = 850 hours
Standard deviation, σ = 70 hours
To find the percentage of batteries that have lifetimes between 710 and 990 hours, we have to find:
![P(710This can be simplified as follows:[tex]\begin{gathered} P((710-850)/(70)Using the standard normal table, we have that:[tex]\begin{gathered} 0.97725-0.02275 \\ \\ 0.9545\Rightarrow95\% \end{gathered}]()
Hence, 95% of batteries have lifetimes between 710 hours and 990 hours.
(b) The middle 68% of the score represents:
![P(-zWe can rewrite this as:[tex]\begin{gathered} P(ZNow, we have to find the z value corresponding to 0.84 from the standard normal table.<p>We have that:</p>[tex]P(Z<0.99)=0.84]()
This implies that:

Using the z-score formula, we have to find the scores corresponding to the z-scores of -0.99 and 0.99.
That is:

For z = -0.99:
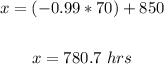
For z = 0.99:
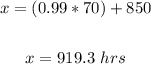
Therefore, approximately 68% of the batteries have lifetimes between 780.7 hours and 919.3 hours.